A max flow approach to course planning
For Dartmouth students, keeping track of one's requirements for graduation is among the most stressful (albiet important) aspects of course planning. There's a whole slew of various credit requirements that some courses fulfill while other don't. Students have the headache of having to mix-and-match many permutations until they allocate their credits optimally.
In building out D-Planner (read my blog on that journey here), we wanted to tackle this tedious process — which we called the "course requirement allocation" problem — with technology so that our platform can automatically and accurately update students on their graduation process.
Course requirement allocation is an optimization problem with many moving parts. To put simply, every student has a set of graduation requirements. Here are the requirements for an example philosophy major.
General education:
- Art: creation, performance, history or criticism; (ART)
- Literature: the history, criticism or theory of texts; (LIT)
- Systems and Traditions of Thought, Meaning and Value; (TMV)
- International or Comparative Study; (INT)
- Social Analysis (two courses); (SOC)
- Quantitative or Deductive Science;(QDS)
- Natural and Physical Science (two courses); without/with lab (SCI/SLA)
- Technology or Applied Science; without/with lab (TAS/TLA)
Major education:
- PHIL 1, 4, 5, 8, 9, or 10
- PHIL 3 or 6
- Two from PHIL 11, 12, 13, 16, or 19
- PHIL 50
- PHIL 80
- Four more general philosophy courses
Every course they complete may satisfy one or more of those requirements. For example, GOVT 5 can either satisfy INT or SOC requirements. GOVT 39, on the other hand, can only satisfy SOC. Hence, a well-planned student should allocate GOVT 5 to INT, and GOVT 39 to SOC to maximize their credits. It's trivial with a few courses; but this problem explodes rapidly in complexity against the entire 36 course Bachelor's program.
Ultimately, this problem can be reduced to the maximum matching problem for a bipartite graph, where requirements are the left side and courses are the right side of the graph. The maximum matching uniquely associates a requirement with a course, and thus provides an optimal course allocation for their plan.
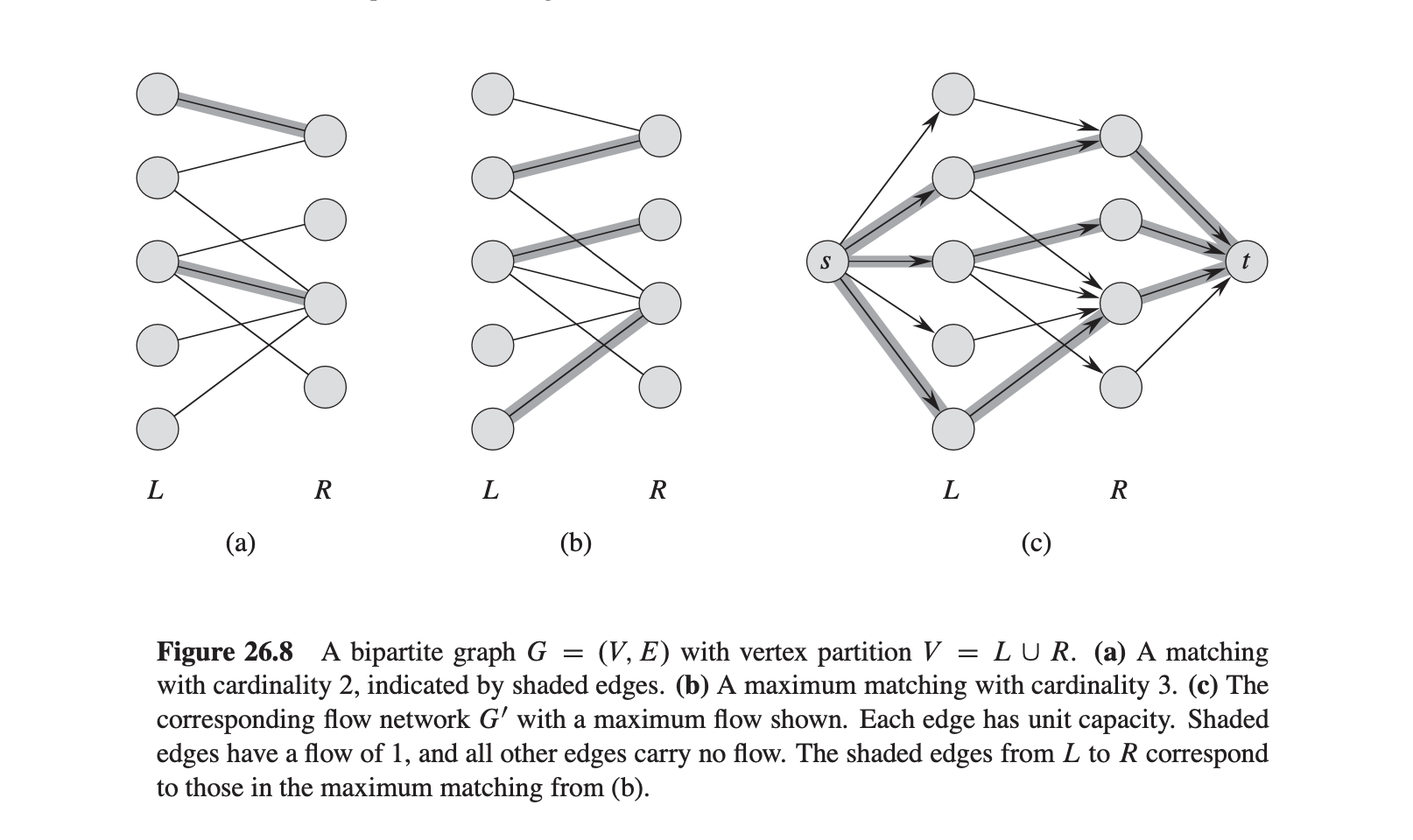
Converting a maximum matching problem to max flow, from CLRS page 733 of the Third Edition.
Luckily, the maximum matching problem can be solved within the graph flow framework. Specifically, if we add a source node and sink node to the left and ride sides of the graph, respectively, we can apply the Edmonds-Karp algorithm to find the maximum flow, which is also the maximum matching.
The Edmonds-Karp approach has a \(O(VE^2)\) time complexity. Dartmouth courses typically fulfill one or two requirements. Therefore, \(|V| \leq |E| \leq 2|V|\). My goal is to re-implement this approach via the Dinic's algorithm algorithm, which instead has \(O(V^2E)\), which is far better suited for the nature of these graphs.
Here is a GitHub Gist that shows how I approached this problem for D-Planner.
| from typing import Deque | |
| # standard degree requirements | |
| DEGREE_REQS = set(['LIT', 'ART', 'SCI', 'TMV', 'TAS', 'INT']) | |
| # course name followed by requirements that it satisfies | |
| courses = { | |
| 'COSC_1': set(['TAS', 'SCI']), | |
| 'GOVT_30': set(['INT', 'TMV']), | |
| 'ENGL_16': set(['LIT', 'INT']), | |
| 'MUSI_80': set(['ART']), | |
| 'PHIL_4': set(['TMV']), | |
| 'BIOL_2': set(['SCI']), | |
| 'ENGS_15': set(['TAS']) | |
| } | |
| def generate_graph(courses: dict[str, set[str]]) -> dict[str, set[str]]: | |
| ''' | |
| Constructs a map of set graph for given courses. | |
| Creates associated flow, capacity, and residual graphs. | |
| ''' | |
| graph = dict() | |
| # add courses to graph | |
| for course in courses: | |
| graph[course] = courses[course] | |
| # add source | |
| graph['SOURCE'] = set([course for course in courses]) | |
| # add sink | |
| graph['SINK'] = set([]) | |
| # add reqs to graph | |
| for req in DEGREE_REQS: | |
| graph[req] = set(['SINK']) | |
| # set up flow, capacities, and residual capacities | |
| flow = {} | |
| cap = {} | |
| res_cap = {} | |
| for u in graph: | |
| flow[u] = dict() | |
| cap[u] = dict() | |
| res_cap[u] = dict() | |
| for v in graph: | |
| cap[u][v] = 1 if v in graph[u] else 0 | |
| flow[u][v] = 0 | |
| res_cap[u][v] = cap[u][v] - flow[u][v] | |
| return graph, flow, cap, res_cap | |
| def find_augmenting_path(res_cap: dict[str, dict[str, int]]) -> list[str]: | |
| ''' | |
| Scopes out the next augmenting path with a breadth search approach. | |
| ''' | |
| to_visit = Deque([('SOURCE', [])]) | |
| while len(to_visit): | |
| (curr, path) = to_visit.popleft() | |
| path.append(curr) | |
| if curr == 'SINK': | |
| return path | |
| # find next nodes with positive residual capacity | |
| nexts = [(next, path.copy()) for next in res_cap[curr] if (res_cap[curr][next] > 0 and next not in path)] | |
| to_visit.extend(nexts) | |
| return None | |
| def fill_requirements(courses: dict[str, set[str]]): | |
| ''' | |
| Given a set of courses and degree requirements, returns an optimal allocation. | |
| ''' | |
| matching = { req: None for req in DEGREE_REQS } | |
| graph, flow, cap, res_cap = generate_graph(courses) | |
| while True: | |
| # get next path | |
| next_path = find_augmenting_path(res_cap) | |
| if next_path is None: | |
| break | |
| # compute lowest flow allowed on path | |
| min_flow_on_path = min([res_cap[next_path[i]][next_path[i + 1]] for i in range(len(next_path) - 1)]) | |
| # augment flow for each edge on path | |
| for i in range(len(next_path) - 1): | |
| u = next_path[i] | |
| v = next_path[i + 1] | |
| flow[u][v] += min_flow_on_path | |
| flow[v][u] = -flow[u][v] | |
| res_cap[u][v] = cap[u][v] - flow[u][v] | |
| res_cap[v][u] = cap[v][u] - flow[v][u] | |
| # save a course-requirement allocation | |
| if u in courses and v in DEGREE_REQS: | |
| matching[v] = u | |
| return matching | |
| def run(): | |
| for course in courses: | |
| print(course + ' gives ' + ', '.join(courses[course])) | |
| print('\ncomputing...\n') | |
| matching = (fill_requirements(courses)) | |
| for req in matching: | |
| print(req + ' fulfilled by ' + str(matching[req])) | |
| run() |
Here's an example allocation generated from this algorithm:
COSC_1 gives TAS, SCI
GOVT_30 gives INT, TMV
ENGL_16 gives LIT, INT
MUSI_80 gives ART
PHIL_4 gives TMV
BIOL_2 gives SCI
ENGS_15 gives TAS
computing...
LIT fulfilled by ENGL_16
ART fulfilled by MUSI_80
TMV fulfilled by PHIL_4
INT fulfilled by GOVT_30
SCI fulfilled by COSC_1
TAS fulfilled by ENGS_15
If these sort of problems fascinates you, join us in building out D-Planner! Reach out to the active maintainers (Ziray Hao, Adam McQuilkin, and Jai Smith) via hello@d-planner.com.